Paillier同态加密

作者：hxd

日期：2025年3月28日

摘要

随着云计算和人工智能的兴起，如何实现安全有效地利用数据，对持有大量数字资产的企业来说至关重要。同态加密，是解决云计算和分布式机器学习中数据安全问题的关键技术，也是隐私计算中，横跨安全多方计算，联邦学习和可信执行环境多个技术分支的热门研究方向。

本文对经典同态加密算法Pailier算法及其相关技术进行介绍，重点分析了Paillier的实现原理和性能优化方案，同时对基于公钥的加密算法中的热门算法进行了横向对比。最后介绍了Paillier算法的一些实际应用。

【关键词】：同态加密，安全多方计算，联邦学习，隐私计算

1 背景知识

1.1 同态加密

同态加密（Homomorphic Encryption，HE）是一种对加密数据进行处理的功能，是一种允许对密文进行计算操作并生成加密结果的加密技术。在密文上获得的计算结果被解密后与在明文上的计算结果相匹配。我的理解是可以在加密的数据上进行计算操作，并且得到的结果解密后与在原始数据上进行相同的计算操作得到的结果一致。

目前，同态加密可以分为三类：部分同态加密（Partially Homomorphic Encryption, PHE）也称为半同态加密、些许同态加密（Somewhat Homomorphic Encryption，SHE）和全同态加密（Fully Homomorphic Encryption, FHE）。半同态加密在数据加密后只持加法运算或乘法运算中的一种，根据其支持的运算的不同，又称为加法同态加密或乘法同态加密。半同态加密由于机制相对简单，相对于全同态加密技术，拥有着更好的性能。全同态加密对加密后的数据支持任意次数的加法和乘法运算。Paillier同态加密是一种半同态加密算法，仅支持加法同态。

1.2 复合剩余类问题

如果存在一个数

$y\in \mathbb{Z}_{n^2}^*$

1.3 二项式定理

二项式定理：$n\in \mathbb{N}^*$

$(a+b)^n=\sum_{r=0}^{n} C^r_{n} a^{n-r}b^r=C^0_{n} a^{n}+C^1_{n} a^{n-1}b+\cdots C^r_{n} a^{n-r}b^r+C^n_{n} b^n$

当$a=1,b=n,n=x$时可以化成下面的形式：

$(1+n)^x=1+nx+\frac{x(x-1)n^2}{2!}+\cdots$

可以化为

$(1+n)^x\equiv 1+nx(\mod n^2)$

令$y=(1+n)^x \mod n^2 $，可化简为$x\equiv \frac{y-1}{n} (\mod n^2)$，再令$L(u)=\frac{u-1}n$

则

$\begin{equation} L\left((1+n)^{x} \bmod n^{2}\right) \equiv L(y) \equiv \frac{y-1}{n} \quad(\bmod n) \equiv x \quad(\bmod n) \end{equation}$

即 $L\left((1+n)^{x} \mod n^{2}\right) \equiv x \quad(\bmod n)$

2 Paillier算法

2.1 密钥生成

类似于RSA算法，Paillier也拥有公钥和私钥对。

随机选择两个大素数$p,q$且$p\ne q$，满足$gcd(pq,(p-1)(q-1))=1$，且满足$p,q$的长度相等。
计算$n=pq$以及$\lambda=lcm(p-1,q-1)$，这里$lcm$表示最小公倍数
随机选择$g\leftarrow \mathbb{Z}_{n^2}^*$
定义$L$函数：$L(x)=\frac{x-1}{n}$，计算$\mu=(L(g^\lambda \mod n^2))^{-1} \mod n$

公钥：$(n,g)$，私钥：$(\lambda,\mu)$

例如：

Alice选择两个大素数$p=11,q=19$
Alice计算$n=p*q=209$，并计算$\lambda=lcm(p-1,q-1)=(10,18)=90$
Alice选择一个随机整数$g=147\in \mathbb{Z}_{n^2}^*$
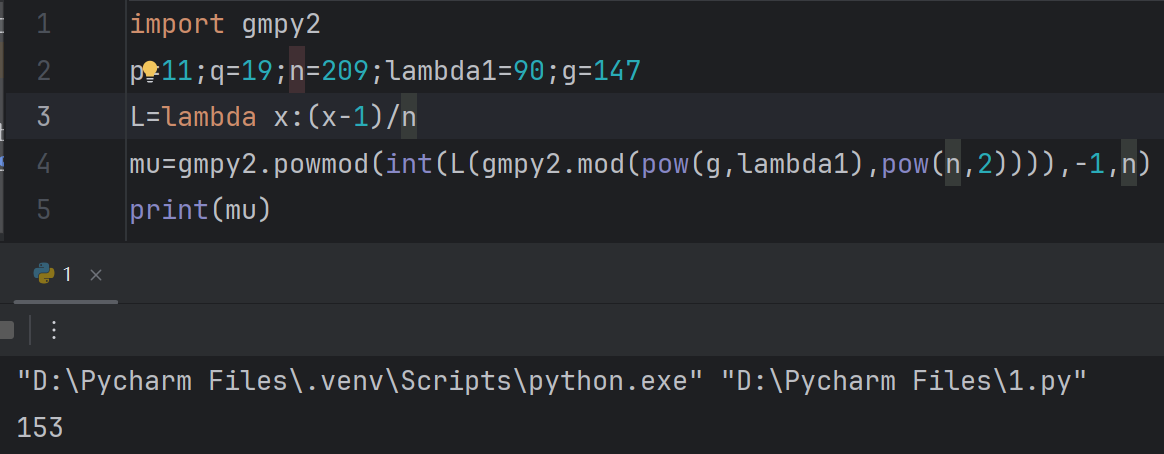
Alice定义函数$L(x)=\frac{x-1}{n}$，计算$\mu=(L(g^\lambda \mod n^2))^{-1} \mod n =153$

所以现在Alice一共生成了6个数字：

$p=11,q=19,n=209,\lambda=90,g=147,\mu=153$

公钥为$(n,g)=(209,147)$，私钥为$(\lambda,\mu)=(90,153)$

import gmpy2
p=11;q=19;n=209;lambda1=90;g=147
L=lambda x:(x-1)/n
mu=gmpy2.powmod(int(L(gmpy2.mod(pow(g,lambda1),pow(n,2)))),-1,n)
print(mu)

2.3.2 加密

输入明文消息$m$，满足$0\le m\le n$
选择随机数$r$满足$0\le r\le n$且$r\in \mathbb{Z}_{n}^*$
计算密文$c=g^mr^n \mod n^2$

例如：

假设Bob需要加密明文$m=8$，且Bob收到了Alice发送来的公钥$(n,g)$
Bob选择随机数$r=3$
Bob计算密文$c=32948$

c=gmpy2.mod(pow(g,m)*pow(r,n),pow(n,2))

2.2 解密

输入密文$c$，满足$c\in \mathbb{Z}_{n^2}^*$
计算明文消息$m=L(c^\lambda \mod n^2))\cdot\mu \mod n$

例如：

Bob发送密文$c$，且$c\in \mathbb{Z}_{n^2}^*$
Alice计算明文$m=L(c^\lambda \mod n^2))\cdot\mu \mod n=8$

m1=gmpy2.mod(L(gmpy2.mod(pow(c,lambda1),pow(n,2)))*mu,n)

2.3 正确性证明

这里可以将$g$进行优化成$g=n-1,\lambda=\varphi(n)=(p-1)(q-1),\mu=\varphi(n)^{-1}\bmod n$

证明如下:

$\begin{equation} Dec(c)=m=L(c^\lambda \bmod n^2))\cdot\mu \bmod n=L((g^mr^n\bmod n^2)^\lambda \bmod n^2))\cdot \mu=L(g^{\lambda m}r^{\lambda n} \bmod n^2))\cdot \mu \bmod n\\ \end{equation}$

根据卡米切尔定理（Carmichael’s function）有：

$r^{\lambda n}\equiv 1\mod n^2$

所以继续化简，且由$L\left((1+n)^{x} \mod n^{2}\right) \equiv x \quad(\bmod n)$知，

$Dec(c)=L(g^{\lambda m}\mod n^2))\cdot \mu \mod n=\lambda m\cdot \mu \bmod n=\lambda m\cdot \frac{1}{\mu}\bmod n=m$

Carmichael number的定义是，对于一个合数 $n$ ，如果所有与 $n$ 互质的正整数 $b$ ，都有 $b^{n-1} \equiv 1\left(\bmod n^{2}\right)$ 成立，则 $n$ 称为Carmichael number。其中 $0<b<n$
$r^{\lambda n} \bmod n^{2}=1$ 其实是Carmichael＇s theorem的一个推论，这里不再详细说明。
对两个数的乘积求余，与对这两个数先求余再相乘的结果相同

2.5 Paillier同态加密性质

2.5.1 加法

$\begin{equation*}Dec(c_1 \cdot c_2 \bmod n^{2})=Dec\left(Enc\left(m_{1}, r_{1}\right) \cdot Enc\left(m_{2}, r_{2}\right) \bmod n^{2}\right)=m_{1}+m_{2} \bmod n \end{equation*}$

这个公式的意思是，明文 $m{1}$ 和 $m{2}$ ，随机选择的加密因子随机数 $r{1}$ 和 $r{2}$ 。 $m{1}$ 和 $m{2}$ 加密后相乘再解密的结果，与 $m{1}+m{2}$ 对 $n$ 求余的结果相同。

2.5.2 乘法

$\begin{align*} & Dec\left(Enc\left(m_{1}, r_{1}\right)^{m_{2}} \bmod n^{2}\right)=m_{1} m_{2} \bmod n \\ & Dec\left(Enc\left(m_{2}, r_{2}\right)^{m_{1}} \bmod n^{2}\right)=m_{1} m_{2} \bmod n \end{align*}$

但是据我了解Paillier同态加密是不支持乘法同态的，仅支持密文乘标量，而不支持密文乘密文。一般地

$\begin{equation*} Dec\left(Enc\left(m_{1}, r_{1}\right)^{k} \bmod n^{2}\right)=k m_{1} \bmod n \end{equation*}$

2.5.3 证明

加法证明:

$\begin{gather*} Enc\left(m_{1}, r_{1}\right)=c_{1}=g^{m 1} \cdot r_{1}^{n} \bmod n^{2} \\ Enc\left(m_{2}, r_{2}\right)=c_{2}=g^{m 2} \cdot r_{2}^{n} \bmod n^{2} \\ c_{1} \cdot c_{2}=g^{m_1+m_2} \cdot\left(r_{1} \cdot r_{2}\right)^{n} \bmod n^{2} \\ Dec\left(c_{1} \cdot c_{2}\right) \equiv L\left(g^{\lambda\left(m_{1}+m_{2}\right)} \cdot\left(r_{1} \cdot r_{2}\right)^{\lambda n} \bmod n^{2}\right) \cdot \mu \bmod n \\ \equiv \lambda\left(m_{1}+m_{2}\right) \cdot \mu \quad(\bmod n) \\ \equiv m_{1}+m_{2} \quad(\bmod n) \end{gather*}$

其中 $\left(r{1} \cdot r{2}\right)^{\lambda n} \equiv 1\left(\bmod n^{2}\right)$ ，依然是利用Carmichael＇s theorem。也不要忘了 $\mu=\lambda^{-1}$ 。加法证毕。

乘法证明:

$\begin{gather*} & Enc\left(m_{1}, r_{1}\right)^{m_{2}} \bmod n^{2}=c_{1}^{m_2}=(g^{m_1} \cdot r_{1}^{n})^{m_2} \bmod n^{2} \\ & Dec\left(Enc\left(m_{1}, r_{1}\right)^{m_{2}} \bmod n^{2}\right)=Dec\left(c_{1}^{m_2}\right)=L(g^{\lambda m_1} \cdot r_{1}^{\lambda n})^{m_2} \bmod n^{2}=L(g^{\lambda m_1 m_2} \cdot r_{1}^{\lambda n m2})\cdot \mu \bmod n^{2}=\lambda(m_1m_2)\cdot \mu=m_1m_2\\ & Enc\left(m_{2}, r_{2}\right)^{m_{1}} \bmod n^{2}=c_{2}^{m1}=(g^{m 2} \cdot r_{1}^{n})^{m1} \bmod n^{2}\\ & Dec\left(Enc\left(m_{2}, r_{2}\right)^{m_{1}} \bmod n^{2}\right)=Dec\left(c_{2}^{m_1}\right)=L(g^{\lambda m_2} \cdot r_{2}^{\lambda n})^{m_1} \bmod n^{2}=L(g^{\lambda m_1 m_2} \cdot r_{1}^{\lambda n m2})\cdot \mu \bmod n^{2}=\lambda(m_1m_2)\cdot \mu=m_1m_2 \end{gather*}$

2.6 Paillier实战

这里主要是使用python-paillier开源库进行模拟, 地址: python-paillier

2.6.1 安装python-paillier库

pip install phe

2.6.2 基本用法

测试代码如下：

from phe import  paillier
from phe.command_line import encrypt

#生成私钥和公钥
public_key,private_key=paillier.generate_paillier_keypair()

secret_number_list=[3.141592653,50000,-4.6e-12]

#加密
encrypted=[public_key.encrypt(x) for x in secret_number_list]
a,b,c=encrypted #a,b,c为分别对应的密文
#解密
decrypted=[private_key.decrypt(x) for x in encrypted]
#print(decrypted)
print("原始的明文数据是:",secret_number_list)
print(f"加密后的密文为:\n{a.ciphertext()}\n{b.ciphertext()}\n{c.ciphertext()}\n")

#直接在密文上进行操作
print("直接在密文上进行加法+2操作:")
for x in encrypted:
    print(private_key.decrypt(x+2))
print("直接在密文上进行乘法*2操作:")
for x in encrypted:
    print(private_key.decrypt(x*2))

#测试加法同态和乘法同态
#同态加密就是直接在密文上进行计算操作，且得到的结果解密后与原始数据进行相同计算操作得到的结果一致
if(private_key.decrypt(a+b)==secret_number_list[0]+secret_number_list[1]):
    print("加法同态得到结果一致")
#不支持密文*密文操作

运行结果：

原始的明文数据是: [3.141592653, 50000, -4.6e-12]
加密后的密文为:
6135642717476440288407940386973406424179597264131770247248102742010468720333833225649509063748135593417249291664647230118171880275385427768661278194179811149980484107875079167966037640330927833409551348424009960068423059960154838566322299195353397421437872915804745060533261832278429271204744456789961203266052848010919722959341417482024982142102529926890593903314112664543957037887158716744571871264210589446764218013112820393615950957086607861565308016365237196306966010745077365412367839307532518170100179456773127734147346604235844813044265233075016539928080838485143223995802554571383461035263995403783064611306317555256285988840969029742977968144872682458936420127227230476819291303124001473587923460769397658268024400886555390258660618373303414439455211672717812666697638035222117443908650283514435608463625378214050364068755129824410490701664831571275306964067204071005470027118378689651829148880539573822487153481061470277580577600175521806242106858972388994227724395869506642559032895967293793343876890145360440625385914915118257143910111826237187307820978010483113189911368282892421162883412638039297069837343163912708762909713756179690176457109522301379897744926757752311597922050024148761665375103555182414838633525445609661410252899063498510115771914132805409567484187921658398974418382890964839125981586348726045243333495314428481282190467375523460497432128692207506441289627508380795234964885871582085230280132691345948398132555966200855244255648321920131951439696611676124269404466976180294962281445458807943012918012404089846508333274591599727485060331623606174040694791503822698059396853307777347504952896153744082791225468534691438132909249689191233089350038971418419335809120903150499784609969567112545363360198125593245665624566815113695011787411604336491361460042949730556105104860435984770859626375877623884062067189129950180
887005022522579447848205920806710360909905718591189281931160414910549152523241076199319838555395628981196313249650442055291336440727334264609927402686839092259539091806267508731596185601945267340158283814725867055142350838873977884437455988256793834938544399110653821598343100566315517131009630463758427674741632987854143941273277406130544928639596805847903901872619306943467440651124331358414655009038819086417786999141500468891038595923333543228285676618955025241632566941244513073724178810891249994862641467055938701921034463570669407425499466966614995736403620307164619068695077483394674655491668059501289997984748471727455510282488950427021066786988802714724934069315750072430493670702292961959351861990350908010035027235436142496519572061639045766037724040168016634665220315171534601878486078146141036209112753667794836310776413372090360499415335386249693576221646721388111593525013348622038294276700011838623658512860535722955926153513295870279541110526588704213026487898973565504365143192106523282754721704597946528197131102310494268027064892280655944273426061769686315420030387006946764328759186228215890918819632830165788070069840471094460082378686670731840685542630431810339310104136600202543862750484297465773842549039973676782156504118923176398442761632823191417959286488765026652099790923996485356416436227426568760028842792661257638755706242281259745653462582679989619677046541678862053832610084198972899069941746702241883580322136635072016411615020395158346898642764436395616200752755431700573294891784344134726676362530310448752821280044944859856437724872997808669615929491594710408026028211363505886848089977144357763600878248532335971494244646237482683583560221949882212204132473662202602957427603105175985896686514125329220361852710593844658262087288692429013917912788736677741102128337897654661912656981245063891143413271880198
4037834938559113619998421172126988631404057769776394076009642746492930549963427577763531697013121860978579303640942002203573909988758058637783285612984589563341275746505104066786459644139296154989247555286766332632956277526381221905394405047878853819672351319589245550064992212014659527107405496539715766902603145770139269460891688467495430592590109629243358486012139563568091165337492106001695221963062782387101039883902482021844332025477744754094691117955989515071972713229143707017639271181111758343051392150486122301639851781824768663450374570863934194319372897693598980087567991904726792217639572484515329384708058640520702920356676765045039269097405323207102964402256931020225226574796100098393728445500536230857645017388597635343797974623015219437794113364384121571373446465230310133314591493338351772191359455173800995719951869852495461808153822475333168253753478440159263287430264597640183391855918546893101611046809590097041491211129504239765147502244593473087877341414822274679881047552475492207704048970711469190320750078378942213065783986762161609262844273973580105444131146141091913501127480420309827038824652233093197954777717602547166876425118434350400560848462197198332051713282037170254544403656446710150866640615337026352654671865687758120421675024795483426165854979402460251083766743824236705890427680912489990719801474531552377098780868655341869341506050884129178193807619968296450530661258034692933951102120282490300045565528259615887430240284882048366613762768924291240487713709102291659985373901417584488360396271364473451620447795773907199476071956478187939530636081184148667494643604921345971538250781793067325928447552265330527703761935250265847640143558212289976423426290977866451255574548301724673646029516803256160958927650871855915629377334996810457919664025499656727666953298009410893931657899407241861948032341341509

直接在密文上进行加法+2操作:
5.141592653
50002
1.9999999999954
直接在密文上进行乘法*2操作:
6.283185306
100000
-9.2e-12
加法同态得到结果一致